│¬╕≡ └Ñ┐í╡≡┼═ 3.0 (╟╤▒█╞╟) ╝÷╜─ ╞φ┴²▒Γ ╗τ┐δ ╣µ╣²

1. ╝÷╜─ ╞φ┴²▒Γ

│¬╕≡ └Ñ┐í╡≡┼═ 3.0┐í╝¡┤┬ "╝÷╜─ ╞φ┴²▒Γ"╕ª └╠┐δ╟╧┐⌐ ╝÷╟╨╜─└╗ ╝╒╜▒░╘ └╘╖┬╟╧░φ ╞φ┴²╟╧░φ └Ñ ╝¡╣÷╖╬ ├Γ╞╟╟╥ ╝÷ └╓└╕╣╟╖╬, └╠░°░Φ └Ñ ╣«╝¡ └█╝║ ╚»░µ└╠ ╚╬╛└ ╞φ╕«╟╪┴│╜└┤╧┤┘. ╝÷╜─ ╞φ┴²▒Γ┤┬ TeX/LaTeX ╣«╣²(╜║┼⌐╕│╞«)└╗ ╗τ┐δ╟╧╕τ, ╝÷╜─└╠ ╞≈╟╘╡╚ ╛╞╖í╛╞ ╟╤▒█ ╞─└╧└╗ └╨└╕╕Θ TeX ╜║┼⌐╕│╞«╖╬ ╣┘▓┘╛ε └Ñ┐í╡≡┼═┐í╝¡ ╟Ñ╜├╟╒┤╧┤┘.

│¬╕≡ └Ñ┐í╡≡┼═└╟ ╝÷╜─ ╞φ┴²▒Γ┤┬ "║±┴╓╛≤ ╕≡╡σ"┐═ "╜║┼⌐╕│╞« ╕≡╡σ"░í └╓╜└┤╧┤┘. "║±┴╓╛≤ ╕≡╡σ"┐í╝¡┤┬ ╕╢┐∞╜║ ┼¼╕»╕╕└╕╖╬ ╝÷╜─ ▒Γ╚ú╕ª └╘╖┬╟╥ ╝÷ └╓└╕╕τ "╜║┼⌐╕│╞« ╕≡╡σ"┐í╝¡┤┬ "TeX/LaTex" ╣«╣²└╕╖╬ ╡╚ ╜║┼⌐╕│╞«(\╕φ╖╔╛ε \╕φ╖╔╛ε ...)╕ª └╘╖┬╟╧╕Θ ╝÷╜─└╗ ╟Ñ╟÷╟╥ ╝÷ └╓╜└┤╧┤┘.

2. ╝÷╜─ ╞φ┴²▒Γ└╟ ╞»┬í

║±┴╓╛≤ ╕≡╡σ╕ª └╠┐δ╟╧╕Θ TeX ╣«╣²└╗ ╕≡╕ú┤┬ ├╩║╕└┌╡╡ ╝÷╜─└╗ └╘╖┬╟╥ ╝÷ └╓╜└┤╧┤┘.
╟«┤┘┐ε ╡╡▒╕ ╕╖┤δ ╕▐┤║┐í╝¡ ╝÷╜─ ▒Γ╚ú╕ª ╝▒┼├╟╧┐⌐ └╘╖┬╟╥ ╝÷ └╓╜└┤╧┤┘.
LaTeX└╠│¬ HWP┐í╝¡ └█╝║╟╤ ╝÷╜─└╗ ║»╚»╟╧┐⌐ └╨╛ε╡Θ└╠╣╟╖╬, └╠╣╠ └█╝║╡╚ ╝÷╜─╡Θ└╗ ▒╫┤δ╖╬ ╗τ┐δ╟╥ ╝÷ └╓╜└┤╧┤┘.

3. ║±┴╓╛≤/╜║┼⌐╕│╞« └╘╖┬ ╣µ╣²

║±┴╓╛≤ ╕≡╡σ┐í╝¡ ▒Γ╚ú╕ª ╝▒┼├╟╘└╕╖╬╜ß ╝÷╜─ ╟Ñ╟÷

╜║┼⌐╕│╞« ╕≡╡σ┐í╝¡ ╜║┼⌐╕│╞«╕ª └╘╖┬╟╘└╕╖╬╜ß ╝÷╜─ ╟Ñ╟÷

4. └Ñ┐í╡≡┼═└╟ ╝÷╜─ ╞φ┴²▒Γ┐í╝¡ ╗τ┐δ ░í┤╔╟╤ ╝÷╟╨ ▒Γ╚ú

1. ▒╫╕«╜║ ╣«└┌

\alpha	\beta	\gamma	\delta	\epsilon	\varepsilon
\zeta	\eta	\theta	\vartheta	\iota	\kappa
\lambda	\mu	\nu	\xi	\pi	\varpi
\rho	\sigma	\varsigma	\tau	\upsilon	\phi
\varphi	\chi	\psi	\omega

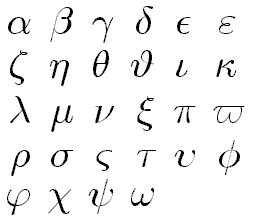
\Gamma	\Delta	\Theta	\Lambda	\Xi	\Pi
\Sigma	\Upsilon	\Phi	\Psi	\Omega

2. ▒Γ╚ú╡Θ

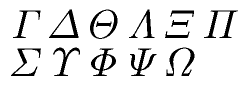
╝÷╜─└╗ ╟Ñ╟÷╟╧▒Γ └º╟╪ ┤┘└╜░· ░░└║ ░ó┴╛ ▒Γ╚ú╡Θ└╗ ╗τ┐δ╟╥ ╝÷ └╓╜└┤╧┤┘.

\aleph	\hbar	\imath	\jmath	\ell	\wp
\Re	\Im	\partial	\infty	\prime	\emptyset
\nabla	\surd	\top	\bot	\smallint	\angle
\triangle	\backslash	\forall	\exists	\neg	\flat
\natural	\sharp	\clubsuit	\diamondsuit	\heartsuit	\spadesuit
\S	\P

3. └╠╟╫ ┐¼╗Ω└┌

└╠╟╫ ┐¼╗Ω└┌┤┬ +, - ╡ε░· ░░└╠ ┤┘╕Ñ ╡╬ ╟╫╕± ╗τ└╠┐í ╡Θ╛ε░í┤┬ ┐¼╗Ω└┌└╘┤╧┤┘. └╠╟╫ ┐¼╗Ω└┌┤┬ ╝÷╜─└╗ ╝÷╜─┤Σ░╘ ╟Ñ╟÷╟╧▒Γ └º╟╪ ║╕┼δ└╟ ▒Γ╚ú┐═┤┬ ┤▐╕« ╛╒╡┌┐í ┐⌐╣Θ└╗ ░í┴²┤╧┤┘.

\triangleright	\triangleleft	\star	\cdot	\times	\ast
\div	\diamond	\pm	\mp	\oplus	\ominus
\otimes	\oslash	\odot	\bigcirc	\circ	\bullet
\bigtriangleup	\bigtriangledown	\cup	\cap	\uplus	\wedge
\vee	\setminus	\wr	\amalg	\sqcap	\sqcup
\dagger	\ddagger

4. ░ⁿ░Φ ┐¼╗Ω└┌

└╠╟╫ ┐¼╗Ω└┌┐═ ░░└╠ ╛╒╡┌╖╬ ┐⌐╣Θ└╗ ░í┴²┤╧┤┘. ┤┘╕╕ ┐⌐╣Θ└╟ ┼⌐▒Γ░í ┤┘╕ª ╝÷ └╓└╕╕τ ║╬┴ñ└╗ │¬┼╕│╗┤┬ ╗τ╝▒└╗ ░í┴· ╝÷ └╓╜└┤╧┤┘.

\smile	\frown	\asymp	\equiv	\subseteq	\supseteq
\leq	\geq	\preceq	\succeq	\sim	\approx
\subset	\supset	\ll	\gg	\prec	\succ
\simeq	\propto	\in	\ni	\not	\mapsto
\perp	\vdash	\dashv	\sqsubseteq	\sqsupseteq

5. ╚¡╗∞╟Ñ╡Θ

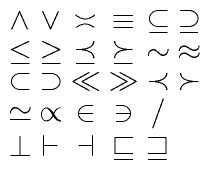
╚¡╗∞╟Ñ┤┬ ░ⁿ░Φ ┐¼╗Ω└┌└╟ └╧┴╛└╕╖╬ ┤┘╛τ╟╤ ╣µ╣²└╕╖╬ ╗τ┐δ╟╥ ╝÷ └╓▒Γ ╢º╣«┐í ╡√╖╬ ║╨╖∙╟╒┤╧┤┘.

\leftharpoonup	\leftharpoondown	\rightharpoonup	\rightharpoondown	\leftarrow	\rightarrow
\uparrow	\downarrow	\leftrightarrow	\nearrow	\searrow	\Leftarrow
\Rightarrow	\Uparrow	\Downarrow	\Leftrightarrow	\nwarrow	\swarrow
\mid	\parallel	\updownarrow	\Updownarrow

6. ┼½ ┐¼╗Ω└┌

┼½ ┐¼╗Ω└┌┤┬ └√║╨▒Γ╚ú ░░└╠ ╡╢╕│ ╝÷╜─(display style)└╕╖╬ ╗τ┐δ╟╥ ░µ┐∞ ┤┘╕Ñ ┼⌐▒Γ╕ª ╗τ┐δ╟╒┤╧┤┘. ╢╟╟╤ ╟╒╗Ω ▒Γ╚ú(sigma)┐═ ░░└╠ └º├╖└┌┐═ ╛╞╖í├╖└┌└╟ └º─í░í ║»╟╧▒Γ╡╡ ╟╒┤╧┤┘.

\sum	\prod	\coprod	\int	\oint
\bigcap	\bigcup	\bigsqcup	\bigvee	\bigwedge
\bigodot	\bigotimes	\bigoplus	\biguplus

╡╢╕│ ╝÷╜─┐í╝¡ ┼½ ┐¼╗Ω└┌┐í ┤δ╟╪ ├╖└┌╕ª ╗τ┐δ╟╤ ┐╣└╘┤╧┤┘. ┐¼╗Ω└┌└╟ ┴╛╖∙┐í ╡√╢≤ ├╖└┌╡Θ└╠ ║┘┤┬ └º─í░í ┤┘╕Ñ ░═└╗ ╛╦ ╝÷ └╓╜└┤╧┤┘.

7. ░²╚ú╡Θ(delimiter)

╝÷╜─└╗ ╟Ñ╟÷╟╧▒Γ └º╟╪ ┤┘└╜░· ░░└║ ░ó┴╛ ▒Γ╚ú╡Θ└╗ ╗τ┐δ╟╥ ╝÷ └╓╜└┤╧┤┘.

(	)	[	]	\{	\}
\lfloor	\rfloor	\lceil	\rceil	\langle	\rangle
/	\backslash	\\|	\uparrow	\downarrow	\updownarrow
\uparrow	\downarrow	\updownarrow	\|

8. ╛╫╝╛╞«

\hat{a}	\breve{a}	\grave{a}	\bar{a}	\dot{a}
\check{a}	\acute{a}	\tilde{a}	\vec{a}	\ddot{a}

9. └σ╜─╡Θ

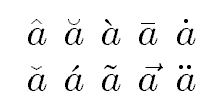
\overline{abc}	\underline{abc}	\overbrace{abc}	\underbrace{abc}
\widehat{abc}	\widetilde{abc}	\overleftarrow{abc}	\overrightarrow{abc}

10. ┐⌐╣Θ╡Θ

\,	\:	\;	\!	\quad	\qquad
░í┤┬ ┐⌐╣Θ	┴▀░ú ┐⌐╣Θ	╡╬▓¿┐ε ┐⌐╣Θ	┐⌐╣Θ ┴┘└╠▒Γ	M ┼⌐▒Γ└╟ ┐⌐╣Θ	M ┼⌐▒Γ ╡╬ ╣Φ└╟ ┐⌐╣Θ

11. ╟╘╝÷ └╠╕º╡Θ

║╕┼δ ╝÷╜─┐í╝¡ ╗τ┐δ╟╧┤┬ ▒█▓├└╗ ┐╖└╕╖╬ ╛α░ú ▒Γ┐∩╛ε┴° └╠┼┼╕» ▒█▓├└╠┴÷╕╕, sin, cos ░░└║ ╟╘╝÷└╟ └╠╕º└║ ╖╬╕╢└┌╕ª ╗τ┐δ╟╒┤╧┤┘. ╢╟╟╤ sin a┐═ ░░└╠ ╟╘╝÷┐═ ▒╫ └╬╝÷ ╗τ└╠┐í┤┬ ╛α░ú└╟ ┐⌐╣Θ└╗ ├▀░í╟╧┐⌐ ▒╕║╨└╗ ╕φ╚«╚≈ ╟╧░φ └╓╜└┤╧┤┘. └Ñ┐í╡≡┼═└╟ ╝÷╜─ ╞φ┴²▒Γ┐í╝¡┤┬ ┤┘└╜░· ░░└║ ╟╘╝÷╡Θ└╠ └╓╜└┤╧┤┘.

\arccos	\cos	\csc	\exp	\ker	\limsup	\min	\sinh
\arcsin	\cosh	\deg	\gcd	\lg	\ln	\Pr	\sup
\arctan	\cot	\det	\hom	\lim	\log	\sec	\tan
\arg	\coth	\dim	\inf	\liminf	\max	\sin	\tanh

╞»▒Γ╟╥ ╕╕╟╤ ╟╘╝÷╖╬┤┬ lim░í └╓╜└┤╧┤┘. ║╕┼δ└╟ ╟╘╝÷┐í ├╖└┌(_)╕ª ║┘└╠╕Θ ┐└╕Ñ┬╩ ┐╖└╕╖╬ └º─í╟╧░╘ ╡╟┤┬╡Ñ, lim ╟╘╝÷┐í ├╖└┌╕ª ║┘└╠╕Θ ╟╘╝÷ └╠╕º└╟ ╣╪┐í ╟Ñ╜├╡╦┤╧┤┘.

╜║┼⌐╕│╞« ╗≤┼┬┐í╝¡└╟ ╝÷╜─ └╘╖┬

1. ║╨╝÷(frac)

n_0 + \frac{1}{n_1
      + \frac{1}{n_2
      + \frac{1}{n_3
      + \frac{1}{n_4+\cdots}}}}

2. ▒┘╚ú(sqrt)

y=\sqrt{x^2+\sqrt{x+12}}

3. ╣Φ┐¡

\left[
\begin{array}{cccc}
\a_{11} & \a_{12} & \cdots & \a_{1n} \\
\vdots & \vdots & \ddots & \vdots \\
\a_{n1} & \a_{n2} & \cdots & \a_{nn} \end{array}
\right]

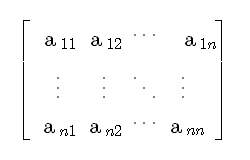
LaTeX└╟ array ╚»░µ░· AmsLaTeX└╟ matrix, pmatrix, bmatrix, dmatrix ╚»░µ└╗ ┴÷┐°╟╒┤╧┤┘.
pmatrix, bmatrix, dmatrix ╚»░µ└║ array ╚»░µ└╟ ┴┬┐∞┐í ░ó░ó ( ), [ ], | | └╟ ▒Γ╚ú╕ª │¬┼╕│╗╕τ, matrix┤┬ ╛╞╣½░═╡╡ │¬┼╕│╗┴÷ ╛╩╜└┤╧┤┘.

4. Eqnarray

\begin{eqnarray}
y & = & x^2 + 1\\
y & > & a - b + c - d + e - f + \\
& & g - h + i - j \nonumber
\end{eqnarray}

┴╓╜─╚╕╗τ │¬╕≡ └╬┼═╖ó╞╝║Ω

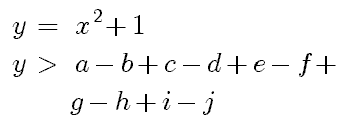
<121-080> ╝¡┐∩╜├ ╕╢╞≈▒╕ ┤δ╚∩╡┐ 485-1╣°┴÷ ║Ñ├│ ║±┴ε┤╧╜║ ╝╛┼═ ╝¡░ⁿ 4├■
e-mail : weinfo@namo.co.kr Fax : (02) 3275-1358